Board Representation

In case you don't know, this is what a chess board looks like:

Starting Chess Board

There are commonly 3 ways a game of chess is programmed. I'll go briefly into the pros and cons of all three methods below.

1. Using a 2D array

Well, when you think of a chess board, it's 8 squares along and 8 squares down, so it makes sense to construct a board like this, right?

[
    [ r n b q k b n r ],
    [ p p p p p p p p ],
    [ . . . . . . . . ],
    [ . . . . . . . . ],
    [ . . . . . . . . ],
    [ . . . . . . . . ],
    [ P P P P P P P P ],
    [ R N B Q K B N R ]
                ^
               here
]

Say you wanted the square where the king's bishop starts. That can easily be represented by the index: [7][5].

However, accessing multiple arrays and especially copying nested arrays (in the event of constructing a decision tree) is very time-consuming and inefficient.

Pros	Cons
Intuitive	Slow, since you need to access two arrays
Easy to update	Positions are two numbers instead of one

2. Using a 1D array

This is a bit better than the 2D array approach, now that you reduce the overhead of accessing two arrays, but it can still be improved.

For a start, when calculating things like rook and bishop moves, you can unintentionally go to the other side of the board when checking squares. On the 2D array, you can easily check that x and y (in [x][y] format) don't exceed either 0 or 7:

def check(x: int, y: int) -> bool:
    return 0 <= x < 8 and 0 <= y < 8

But for a 1D array, you have to either:

manually get an x and y value (using divmod(n, 8)) and check that way
store an array of edge values (like a mask) so you know when to stop

Either way, we can still do better.

3. Using bitboards [the best approach]

A chess board has 64 squares. Most computers can do incredibly fast and optimised operations on 64-bit numbers. Can you see a correlation?

We can use what's called a bitboard to represent our game state. A bitboard is just a binary number that represents some position (or part of a position) of a game. For example, in Connect Four, you can represent this position:

. . . . . . .
. . . . . . .
. . . . . . .
. . . 2 . . .
. . 1 1 . . .
. . 2 1 . . .

With two binary numbers to represent the counters of each player:

# Player 1          # Player 2
. . . . . . .       . . . . . . .
. . . . . . .       . . . . . . .
. . . . . . .       . . . . . . .
. . . . . . .       . . . 1 . . .
. . 1 1 . . .       . . . . . . .
. . . 1 . . .       . . 1 . . . .

We can do the same with chess. Take this position for example:

Random Position

A bitboard representing all the pieces on the board could look like this:

. . . . . . . .
. . 1 . . . . 1
. 1 . 1 . . . 1
. . 1 1 . . 1 .
1 . . . . . . 1
. . 1 1 1 1 . .
. . . . 1 . 1 .
. . . 1 . . . .

For context, I'm using what's known as a Little Endian format for my bitboards. The positions of each bit are laid out like this:

56 57 58 59 60 61 62 63
48 49 50 51 52 53 54 55
40 41 42 43 44 45 46 47
32 33 34 35 36 37 38 39
24 25 26 27 28 29 30 31
16 17 18 19 20 21 22 23
 8  9 10 11 12 13 14 15
 0  1  2  3  4  5  6  7

Move Generation

The first and most important step of the game of chess is moving pieces. How else would you be able to even play a game of chess if not for being able to move pieces?

I'm sure you know about chess (why else would you be reading this?) and the rules on the board. Rules like:

do not lob the board with its pieces at your opponent (at any time).
pawns may not be flicked across the board at your opponent's eyes.
taking the opponent's queen off the board and blowing a rasperry at them is not permitted.

Apologies. Wrong rule list. Just found the right one now:

you cannot castle into check.
bishops cannot move orthogonally.
pawns cannot promote to a king.

So how do we code movement?

Well, consider all the six different types of pieces in the game of Chess:

pawns
knights
bishops
rooks
queens
kings

We can categorise them into two types: static and sliding.

These are explained in doc/move gen [static pieces] and doc/move gen [sliding pieces] respectively. The docs on static pieces should be read first before sliding pieces.

Move Generation [Static Pieces]

This section will explain generating moves for the following pieces:

Kings (using a pregenerated tablebase)
Knights (using a pregenerated tablebase)
Pawns (on the fly)

Explanation

Static pieces have fixed reach limits that will always remain the same, no matter the position. Pawns cannot move backwards, kings cannot move off of the board - you get the idea.

Because these all have fixed rules, we can generate them all once and store them in a table. Here's an example for all king moves.

Code

fileA = 0x101010101010101
fileH = 0x8080808080808080


def get_king_moves(square: int):
    directions = [7, 8, 9, 1]
    moves = 0

    current = 1 << square

    for direction in directions:
        moves |= current << direction
        moves |= current >> direction

    if current & fileA:
        moves &= ~fileH
    
    if current & fileH:
        moves &= ~fileA

    return moves


def create_king_table() -> list[int]:
    return [get_king_moves(square) for square in range(64)]

This is simple enough to understand. Let's dive a little deeper.

Explanation

We have a square parameter, say it's 35, then we shift 1 to that amount to create a bitmask like this:

# bb of 1 << 35
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . 1 . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .

Then we take an empty bitboard (value of 0) then we OR values onto it, which is like pasting bits onto the bitboard.

# current square    # direction: 7      # direction: 8      # direction: 9      # direction: 1
. . . . . . . .     . . . . . . . .     . . . . . . . .     . . . . . . . .     . . . . . . . .
. . . . . . . .     . . . . . . . .     . . . . . . . .     . . . . . . . .     . . . . . . . .
. . . . . . . .     . . 1 . . . . .     . . . 1 . . . .     . . . . 1 . . .     . . . . . . . .
. . . 1 . . . .     . . . . . . . .     . . . . . . . .     . . . . . . . .     . . 1 . 1 . . .
. . . . . . . .     . . . . 1 . . .     . . . 1 . . . .     . . 1 . . . . .     . . . . . . . .
. . . . . . . .     . . . . . . . .     . . . . . . . .     . . . . . . . .     . . . . . . . .
. . . . . . . .     . . . . . . . .     . . . . . . . .     . . . . . . . .     . . . . . . . .
. . . . . . . .     . . . . . . . .     . . . . . . . .     . . . . . . . .     . . . . . . . .

Shifting left moves the bit higher up the bitboard and shifting right moves the bit lower down the bitboard. When combining all four of these bitmasks, we get this:

. . . . . . . .
. . . . . . . .
. . 1 1 1 . . .
. . 1 . 1 . . .
. . 1 1 1 . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .

However, if the square was 32, this is what the moves would look like:

. . . . . . . .
. . . . . . . 1
1 1 . . . . . 1
. 1 . . . . . 1
1 1 . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .

The bits overlap to the other side! To counter this, we include two if statements where if the current square is on the A file, we discard any bits from the H file, and vice versa, resulting in this:

# current bits      # ~fileH            # current & ~fileH
. . . . . . . .     1 1 1 1 1 1 1 .     . . . . . . . .
. . . . . . . 1     1 1 1 1 1 1 1 .     . . . . . . . .
1 1 . . . . . 1     1 1 1 1 1 1 1 .     1 1 . . . . . .
. 1 . . . . . 1     1 1 1 1 1 1 1 .     . 1 . . . . . .
1 1 . . . . . .     1 1 1 1 1 1 1 .     1 1 . . . . . .
. . . . . . . .     1 1 1 1 1 1 1 .     . . . . . . . .
. . . . . . . .     1 1 1 1 1 1 1 .     . . . . . . . .
. . . . . . . .     1 1 1 1 1 1 1 .     . . . . . . . .

We bitwise AND our generated mask against all the bits that are not on the H file, removing all the bits on the H file. We can do a similar thing for the A file with:

if current & fileH:
    current &= ~fileA

We then create a list comprehension of all the bitmasks and store it in a list.

Note: This is written in Python for ease of understanding. Code for a chess engine should be written in a language like C, C++, C# or any other faster language. It is not ideal to use Python for writing a chess engine.

Move Generation [Sliding Pieces]

This section will cover generating moves for the following pieces uisng a technique called magic bitboards:

Bishops
Rooks
Queens

Introduction

Sliding pieces can move in any number of squares along the board, and but their moves are halted if "blockers" are in the way. This is for rooks, bishops and queens.

Take this board occupancy as an example. This is a bitmask of all the pieces on the board.

. . . . . . . .
1 1 1 . 1 . . 1
. . . . . . 1 .
. 1 1 . R . . .
. . 1 . . 1 1 .
. 1 . . . . . 1
. 1 . . 1 . . .
. . . . . . . .

Let's say we know there's a rook on E5 and we want a bitmask of where it can move to. How would we go about that?

We can use the power of magic bitboards for this.

Note: This is going to be a very brief overview of the steps. You can read more into this subject at these two sources:

Magic Bitboards

Explanation

The concept of magic bitboards is four steps (with examples):

Get a mask of the relevant bits in the position

# pieces on board     # relevant bitmask    # resulting bitmask
. . . . . . . .       . . . . . . . .       . . . . . . . .
1 1 1 . 1 . . 1       . . . . 1 . . .       . . . . 1 . . .
. . . . . . 1 .       . . . . 1 . . .       . . . . . . . .
. 1 1 . R . . .   &   . 1 1 1 . 1 1 1   =   . 1 1 . R . . .
. . 1 . . 1 1 .       . . . . 1 . . .       . . . . . . . .
. 1 . . . . . 1       . . . . 1 . . .       . . . . . . . .
. 1 . . 1 . . .       . . . . 1 . . .       . . . . 1 . . .
. . . . . . . .       . . . . . . . .       . . . . . . . .

Multiply this resulting bitmask by a magic number to get an index mapping where all the bits are compiled together.

. . . . . . . .       . . . . . . . .       4 5 A B C D E]
. . . . 5 . . .       . . . . . . . .       . . . .[1 2 3
. . . . 4 . . .       . . . . . . . .       . . . . . . .
. A B C . D E .   *   . .some magic .   =   . . . . . . .
. . . . 3 . . .       . . . bits. . .       . .garbage. .
. . . . 2 . . .       . . . . . . . .       . . . . . . .
. . . . 1 . . .       . . . . . . . .       . . . . . . .
. . . . . . . .       . . . . . . . .       . . . . . . .

Right shift the index mapping by 64-n bits (n is the number of bits in the relevant bitmask) to create a custom index.

4 5 A B C D E]                  . . . . . . . .
. . . .[1 2 3                   . . . . . . . .
. . . . . . .                   . . . . . . . .
. . . . . . .                   . . . . . . . .
. .garbage. .  >> (64 - 10)  =  . . . . . . . .
. . . . . . .                   . . . . . . . .
. . . . . . .                   D E]. . . . . .
. . . . . . .                  [1 2 3 4 5 A B C

Use the index to access a database of pre-generated moves.

rook_moves[square][hashKey]

Implementation

Putting all 4 steps together, we get this:

RELEVANT_ROOK_BITMASKS = [...] # relevant masks fore ach square
ROOK_MAGICS = [...] # 64 magics for each square
ROOK_SHIFTS = [...] # 64 shifts for each magic

# database with moves, set as empty
ROOK_MOVE_TABLE = [[0 for _ in range(4096)] for _ in range(64)]

def shitty_rook_hash(occupancy: int, square: int) -> int:
    occ = occupancy & RELEVANT_ROOK_BITMASKS[square]
    occ *= ROOK_MAGICS[square]
    hashKey = occ >> ROOK_SHIFTS[square]
    return ROOK_MOVE_TABLE[square][hashKey]

As for how we add move masks to the table, this is what we do:

for squarePosition in range(64):
    squares = []
    mask = RELEVANT_BISHOP_BITMASKS[squarePosition]

    while mask:
        LSB = mask & -mask
        squares.append(bit_index(LSB))
        mask ^= LSB
    
    for linearOccupation in range(1 << len(squares)):
        mappedOccupancy = mapLinearOccToSquares(squares, linearOccupation)

        hash = CAP_TO_64_BITS(mappedOccupancy * ROOK_MAGICS[squarePosition]) >> ROOK_BIT_SHIFT

        ROOK_MOVES_TABLE[squarePosition][hash] = traceOutRookMoves(mappedOccupancy, squarePosition)

This is an implementation of plain magic bitboards: the easiest of the batch. However, we can do better.

You can read all about this and the other code here in my gist.

There is a code sample for plain magic bitboards and documentation for it.

Fancy Magic Bitboards

For a start, this nested array system is way too slow. In C#, accessing 2D arrays is 35% slower than 1D arrays so we're adding extra overhead for no reason. What we can do is group a few things together for more efficiency.

Speedup 1: Summing the tables together

Instead of a group of 2D arrays, we can group all the 2D arrays together then include an offset for where to index from. All the arrays have a fixed length of 4096, so we can calculate an offset like this:

def get_rook_moves(occupancy: int, square: int) -> int:
    hashKey = ... # generate hash
    
    offset = square * 4096

    return ROOK_MOVE_TABLE[offset + hashKey]

Speedup 2: Structure of Arrays vs Array of Structures

Currently, the relevant bitmasks, magics and offsets are all in 3 separate arrays, meaning 3 separate accesses. We can group them together in a record to end up with just one array of objects with 3 attributes.

class MagicEntry:
    def __init__(self, mask: int, magic: int, shift: int, offset: int) -> None:
        self.mask = mask
        self.magic = magic
        self.shift = shift
        self.offset = offset

And the C# equivalent in case you're curious.

public record MagicEntry
{
    public ulong mask;
    public ulong magic;
    public ulong shift;
    public ulong offset;

    public MagicEntry(ulong mask, ulong magic, ulong shift, ulong offset)
    {
        this.mask = mask;
        this.magic = magic;
        this.shift = shift;
        this.offset = offset;
    }
}

We can then assemble these into an array then access the array with the square parameter in the function. This way, we have only one lookup in an array then a second for the attacks.

ROOK_ATTACK_TABLE = [...] # 64 * 4096 = 262,144 in length
ROOK_MAGICS: list[MagicEntry] = [...] # 64 rook magics

def get_rook_moves(occupancy: int, square: int) -> int:
    entry = ROOK_MAGICS[square]

    occ = occupancy & entry.mask
    occ *= entry.magic
    key = occ >> entry.shift

    return ROOK_ATTACK_TABLE[entry.offset + key]

Speedup 3: Summing together bishop and rook attack tables

To compact things a bit more, it makes sense to join the rook and bishop tables together, producing a single attacks array of length 262,144 + 32,768 = 294,912. However, because we blended the two tables together, we need to know where one starts and the other stops.

To fix this, we can create a variable called BISHOPS_START_FROM that holds a value of 262,144 then use that as a second offset to the get_bishop_moves() function.

SLIDING_PIECE_ATTACKS_TABLE = [...] # length of 294,912 | [0 for _ in range(294_912)]
BISHOP_MAGICS: list[MagicEntry] = [...]

BISHOPS_START_FROM = 262_144

def get_bishop_moves(occupancy: int, square: int) -> int:
    entry = BISHOP_MAGICS[square]

    ... # hash stuff

    index = BISHOPS_START_FROM + entry.offset + key

    return SLIDING_PIECE_ATTACKS_TABLE[index]

Queen Moves

Queens are a combination of bishop moves and rook moves, so we can use a bitwise OR to combine the bits from both of these.

def get_queen_moves(occupancy: int, square: int) -> int:
    return get_bishop_moves(occupancy, square) | get_rook_moves(occupancy, square)

That's literally all you have to do for queen moves.

Move Generation [Pawns and Tables]

Pawns are quite special pieces. For a start, their attacks are not aligned with their movements, they can promote to a range of pieces at the backrank and they can do a stupid French move that's really cool to watch.

Analysis

# Example of the moves and attacks
# for the pawn on D2
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . 3 . . . .
. . 2 1 2 . . .
. . . P . . . .
. . . . . . . .

As we can see here:

the movement square is listed as 1
the two-spaces pawn push is listed as 3 (because it's optional)
the attack squares are listed as 2's

Note: For this section, I'll be focusing on white pawns. Invert the operations for black pawns.

Left and Right Attacks

The offsets for all the 2 squares are 7 and 9, so we can go up (shift left) by 7 and 9 for white pawns, and go down (shift right) 7 and 9 for black pawns.

leftAttacks  = occupancy & (whitePawns << 7)
rightAttacks = occupancy & (whitePawns << 9)

Problems

Simple, right? Yes. However, we forgot to account for pawns on the A and H files, shown here.

# pawn on A file    # pawn on H file
. . . . . . . .     . . . . . . . .
. . . . . . . .     . . . . . . . .
. . . . . . . .     . . . . . . . .
. . . . . . . .     . . . . . . . .
. . . . . . . .     . . . . . . . .
3 . . . . . . .     . . . . . . . 3
1 2 . . . . . .     . . . . . . 2 1
P . . . . . . .     . . . . . . . P
. . . . . . . .     . . . . . . . .

If we shift the pawns by 9 for the pawn on the A file (7 for on H file), we end up with attacks like this:

. . . . . . . .     . . . . . . . .
. . . . . . . .     . . . . . . . .
. . . . . . . .     . . . . . . . .
. . . . . . . .     . . . . . . . .
. . . . . . . .     1 . . . . . . .
. 1 . . . . . .     . . . . . . 1 .
P . . . . . . 1     . . . . . . . P
. . . . . . . .     . . . . . . . .

This is of course, not legal. You can't attack a piece on the other side of the board. So we need to fix our logic.

Solution

Well, if we get left attacks of all the pawns, the only one we encounter problems with is the one on the A file. (You can verify this yourself in the previous diagram.) So, since that's where our problems are, let's just remove it.

We can exclude all bits on the A file by getting all the bits not on the A file then bitwise ANDing that against the bitmask of the pawns.

Like this:

# example           # ~fileA            # nothing on A file
. . . . . . . .     . 1 1 1 1 1 1 1     . . . . . . . .
. . . . . . . .     . 1 1 1 1 1 1 1     . . . . . . . .
. . . . . . . .     . 1 1 1 1 1 1 1     . . . . . . . .
. . . . . . . .  &  . 1 1 1 1 1 1 1  =  . . . . . . . .
1 . . . . . . .     . 1 1 1 1 1 1 1     . . . . . . . .
. . 1 . . . . 1     . 1 1 1 1 1 1 1     . . 1 . . . . 1
. 1 . . . 1 1 .     . 1 1 1 1 1 1 1     . 1 . . . 1 1 .
. . . . . . . .     . 1 1 1 1 1 1 1     . . . . . . . .

Now we can safely get left attacks without needing to compensate for errors from the A file pawns.

Replication

We can do the exact same thing for the pawns on the H file: when we want to get right attacks, we ignore the pawns on the H file using ~fileH and bitwise ANDing it against the pawn bitmask to get a safe bitmask to check for right attacks on.

Combining everything

leftAttacks  = occupancy & ((pawns & ~fileA) << 7)
rightAttacks = occupancy & ((pawns & ~fileH) << 9)

Single and Double Pushes

Pawns have two other moves we need to account for: moving forward once and moving forward twice, but only on their first move. Keeping track of whether all 8 pawns have moved or not is a bit pointless since we can just check if they're on their start position. Pawns can't move backwards, so once they get moved, they cannot move two spaces again.

Single Pushes

Let's start with single pushes. Pawns move 1 square in front, so we can just shift left by 8. However, if there's a piece in front of the pawn, it cannot move forward.

Take this position for example:

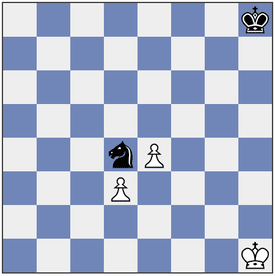
Pawn Pushes Demonstration

As you can see, the pawn on D3 is obstructed by the knight on D4 so it can't move forward. However, the pawn on E4 is not obstructed by anything, so it can move forward.

We can take a board mask of the occupancy on the board, which would look like this:

. . . . . . . 1
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . 1 1 . . .
. . . 1 . . . .
. . . . . . . .
. . . . . . . 1

And then we can take a board mask of all the pawns on the board, which would look like this:

. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . 1 . . .
. . . 1 . . . .
. . . . . . . .
. . . . . . . .

We can shift this bitboard up by 8 to get this:

. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . 1 . . .
. . . 1 . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .

Then do a bitwise NOT on the board mask to get only empty spaces to get this:

1 1 1 1 1 1 1 .
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 . . 1 1 1
1 1 1 . 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 .

And do a bitwise AND against the empty spaces to get only valid pawn pushes.

. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . 1 . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .

And that's it. That's how we can do single pushes.

In code, that looks like this:

singlePushes = ~occupancy & (pawns << 8)

Double Pushes

For double pushes, we could do this:

doublePushes = ~occupancy & (pawns << 16)

However, if there's a piece in the way on the first square, this would still show that you can do a double push, yet the piece is clearly blocking, so we have to revise our answer.

Using Single Pushes

After we push once, all the pawns on the second rank end up where? The third rank. So we can just check for the pawns on the third rank, then do the exact same thing but shifted up 8 higher.

So we do a single push, twice. Sounds stupid, but it works.

With single pushes that look like this:

singlePushes = ~occupancy & (pawns << 8)

We can structure our double push checks like this:

doublePushes = ~occupancy & ((singlePushes & rank3) << 8)

The only difference is swapping the pawns variable with singlePushes & rank3 which gets the single pushes on the third rank with a bitwise AND, then we check if there is a piece blocking us from going to the second square.

And that's it. That's everything.

Complete code sample

leftAttacks  = occupancy & ((pawns & ~fileA) << 7)
rightAttacks = occupancy & ((pawns & ~fileH) << 9)

singlePushes = ~occupancy & (pawns << 8)
doublePushes = ~occupancy & ((singlePushes & rank3) << 8)

Axololly Chess

Board Representation

1. Using a 2D array

2. Using a 1D array

3. Using bitboards [the best approach]

Move Generation

So how do we code movement?

Move Generation [Static Pieces]

Explanation

Code

Explanation

Note: This is written in Python for ease of understanding. Code for a chess engine should be written in a language like C, C++, C# or any other faster language. It is not ideal to use Python for writing a chess engine.

Move Generation [Sliding Pieces]

Introduction

Magic Bitboards

Explanation

Implementation

Fancy Magic Bitboards

Speedup 1: Summing the tables together

Speedup 2: Structure of Arrays vs Array of Structures

Speedup 3: Summing together bishop and rook attack tables

Queen Moves

Move Generation [Pawns and Tables]

Analysis

Left and Right Attacks

Problems

Solution

Replication

Combining everything

Single and Double Pushes

Single Pushes

Double Pushes

Using Single Pushes

Complete code sample

Unfinished.

Unfinished.

Unfinished.